Quantum Marriage Proposal

png

Quantum computing is very different from the classical computing we are all used to. I realized that the day I decided to learn the basics of this amazing field and write a simple Hello World! program. It is not just about printing a string on the screen, but about using the properties of Quantum Mechanics to solve a particular problem. I needed to come up with creative problem to solve!

I found one:

Months ago I proposed to my girlfriend Mari. Like in the quantum world of atoms and electrons, Mari was in a superposition state, a equal-weighted combination of two states: "Yes" and "No".

Then, one day I had the courage to measure the state. This step forced the reveal of the final state.

Yes, a proposal as a quantum problem.

Defining the answers:

As explained before there are two possible answers. To represent those I am going to use the binary representation of characters Y and N.

They are 8 bits long. As shown below, the bits in position 0, 1, 2 and 4 are exchanged. Only 4 bits that, depending on their values, could make the proposal day the best or the worst of my life. Pretty scary if you think about it.

print(bin(ord('Y')))
print(bin(ord('N')))

0b1011001
0b1001110

Preparing the Quantum Circuit:

To represent and solve this problem I need:

The classical bits will be used to store the results of the measurement of each individual qubit.

In order to put together the qubits, bits and gates I will also need a Quantum Circuit. This circuit will be used to collect the answer to our question.

To make the concept clear, here is a representation of Quantum Circuit with 1 qubit and 1 classical bit.

png

from qiskit import ClassicalRegister, QuantumRegister, QuantumCircuit, execute
from qiskit.tools.visualization import plot_histogram, circuit_drawer

# 8 Qubits
q = QuantumRegister(8)

# 8 Classical bits
c = ClassicalRegister(8)

# 1 Quantum Circuit
qc = QuantumCircuit(q, c)

Initial state of the qubits:

By default qubits start with a value of 0, that corresponds to lowest energy state. So, the qubit representation is 00000000. In order to change it to the binary value of Y, that is 01011001, I would need to bit-flip the bits in position 0, 3, 4 and 6. This is done with a X Gate, that in classic computing is represented with a NOT gate.

qc.x(q[0])
qc.x(q[3])
qc.x(q[4])
qc.x(q[6])

The current representation is 01011001 or "Y"

The negative answer

Right now I have prepared the initial state of our 8 qubits to represent the character Y. This is cheating! If I measure the final of each qubit I will always get an affirmative answer to my question. So I need to add the second terrible option. I need to really know what is the answer, and it could also be N.

As I explained before, the difference between the two answers are only in the positions 0, 1, 2 and 4:

Y: 01011001

N: 01001110

I need the qubits in the same position entangled so they can produce both values.

Entanglement and Superposition:

Entanglement is a pretty amazing quantum phenomena. Two or more quantum objects behave individually random while still being strongly correlated, even when separated by a large enough distance to influence one another. In this case they need to be described as a whole instead of independently.

In other words, when I entangle two qubits, measuring one of them will behave randomly. But this random behaviour will allow to predict how the other qubit will behave.

Yes, difficult to understand and even more difficult to explain.

So let's go step by step.

First I will need a qubit that behaves randomly. This can be done by creating a superposition. In a superposition state, the qubit is neither 0 or 1, but a combination of these two states. In other words, when I read its final state the output will be random. To put a qubit in superposition state I will use a H gate:

qc.h(q[1])

Now that the qubit 1 is in superposition, I will entangle it with the one in position 2.

This is done with a Controlled-NOT gate. This gate connect two qubits, the control and the target one.

If the value of the control qubit is 1, then the target will flip its value.

For example, let's say that I have two pairs of qubits. The one in the first position is the control and the one in the second position is the target. This would be the result of applying a Controlled-NOT gate.

00 C-NOT=> 00
01 C-NOT=> 01
10 C-NOT=> 11
11 C-NOT=> 10

So basically now I need to entangle the remaining bits so the output can produce Y and N.

qc.cx(q[1],q[2])
qc.cx(q[2],q[0])
qc.cx(q[0],q[4])

Now I have a qubit that is random, but correlated to others thanks to the entanglement between them. By measuring the random final stage I can predict the value of the other qubits.

Asking the question:

Let's measure the final stage from the Quantum Circuit, or using other words, let's ask the question! Not once, but many times.

The different answers will be measured by their probabilities:

for j in range(8):
    qc.measure(q[j], c[j])

job_sim = execute(qc, "local_qasm_simulator")
sim_result = job_sim.result()
result = sim_result.get_counts(qc)

result["Yes"] = result.pop('01001001')
result["No"] = result.pop('01011110')
print(result)
plot_histogram(result)

png

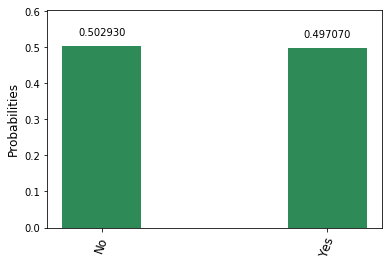
Most of you are thinking that this is not very clear answer, but in the Quantum world it actually is!

import matplotlib.pyplot as plt
plt.rc('font', family='monospace')

fig = plt.figure()
fig.suptitle('The answer in the Quantum World', fontsize=14, fontweight='bold')

ax = fig.add_subplot(111)
plt.axis('off')

ay = result["Yes"]/100
an = result["No"]/100

ax.text(3, 1, 'Y', fontsize=280, alpha=ay)
ax.text(3, 1, 'N', fontsize=280, alpha=an)

ax.axis([0, 10, 0, 10])

plt.show()

png

Fortunately I asked the question in a bigger world. The answer I got... Y.

jpeg

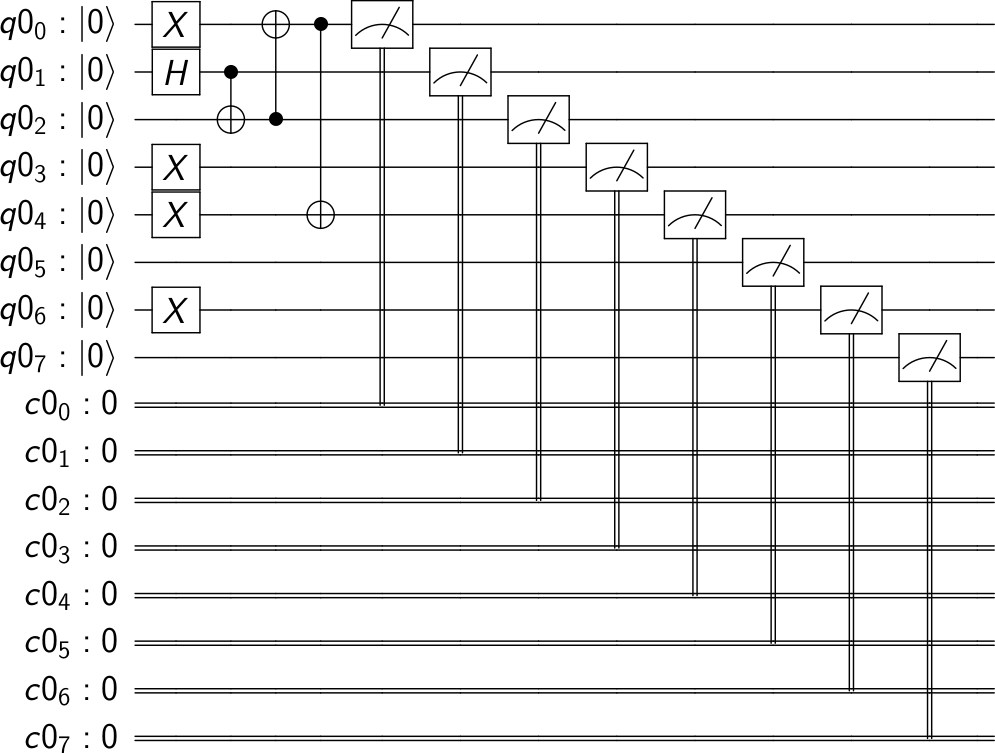
Quantum Circuit Schema

As a bonus, this is the representation of the Quantum Circuit Schema.

circuit_drawer(qc)

png

Credits:

I got the idea from:

Thank you IBM for all the amazing resources available in IBM Q Experience!